Originally published in 2009 at http://www.math.ucla.edu/~rcompton/musical_gauss_seidel/musical_gauss_seidel.html

One second of a 44.1kHz single channel .wav file can be read into an array (call it b) of length 44100. Given a matrix A we seek solutions to the system Ax=b. Through iterations of Gauss-Seidel the vector Ax will approach b with the high frequency parts of Ax getting close to b first. If we take b to be a song recording, some white noise as our initial guess and write out Ax at each iteration we observe that the high pitched notes in b become audible first while at the same time the pitch of the white noise decreases.

Audio of the initial 12 second .wav file (white noise) initialAx.wav

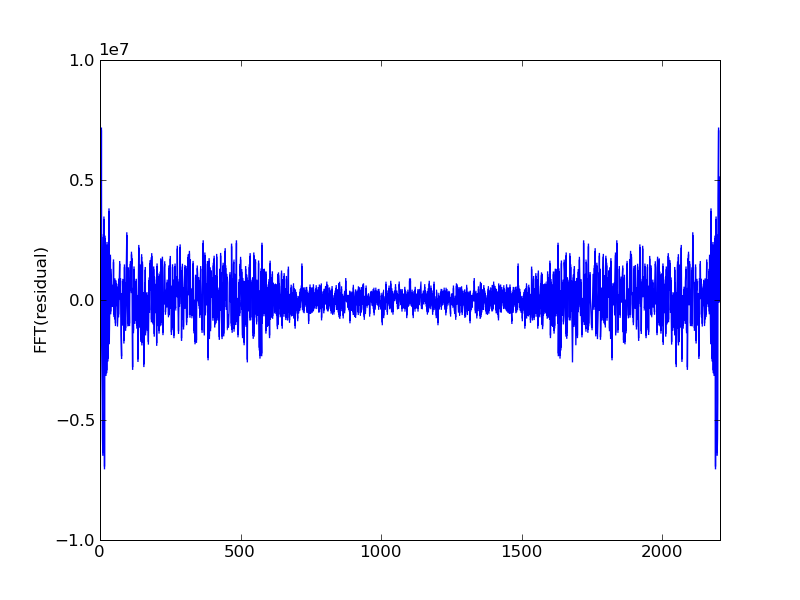
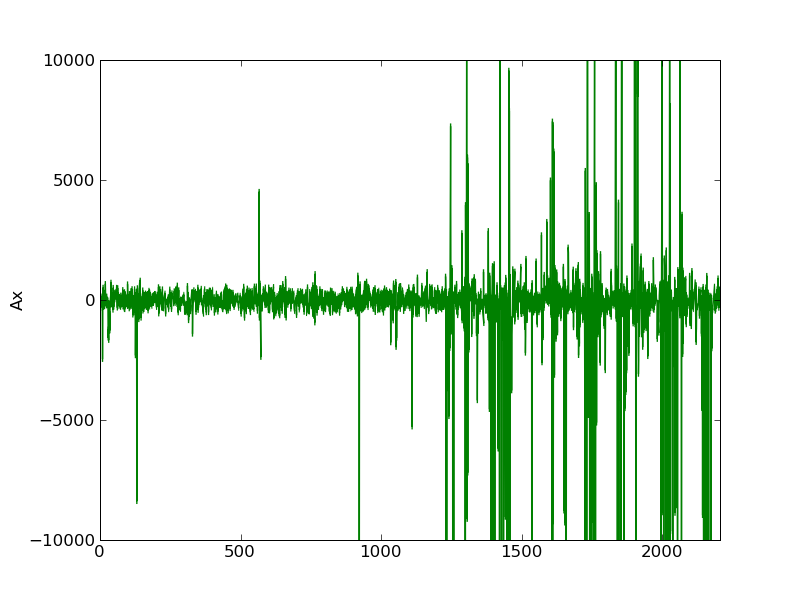
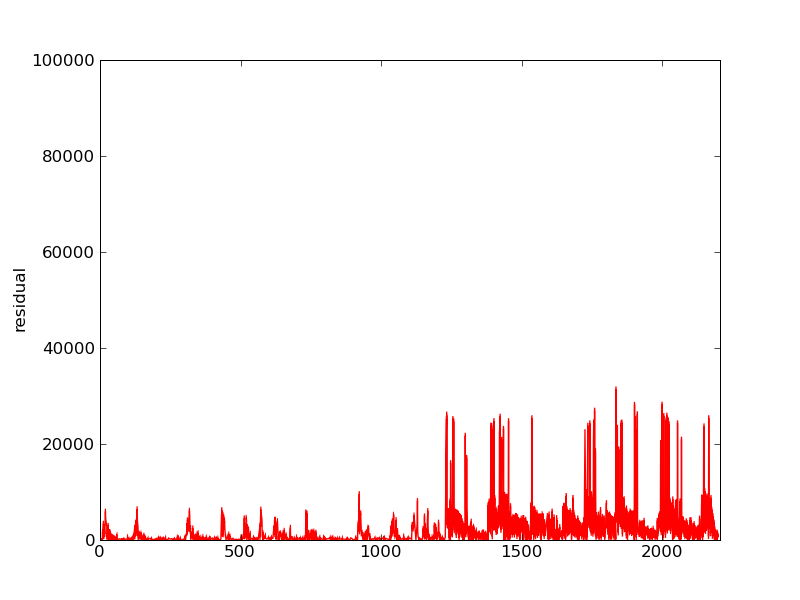
Plots of the initial Ax, residual, and FFT of residual:

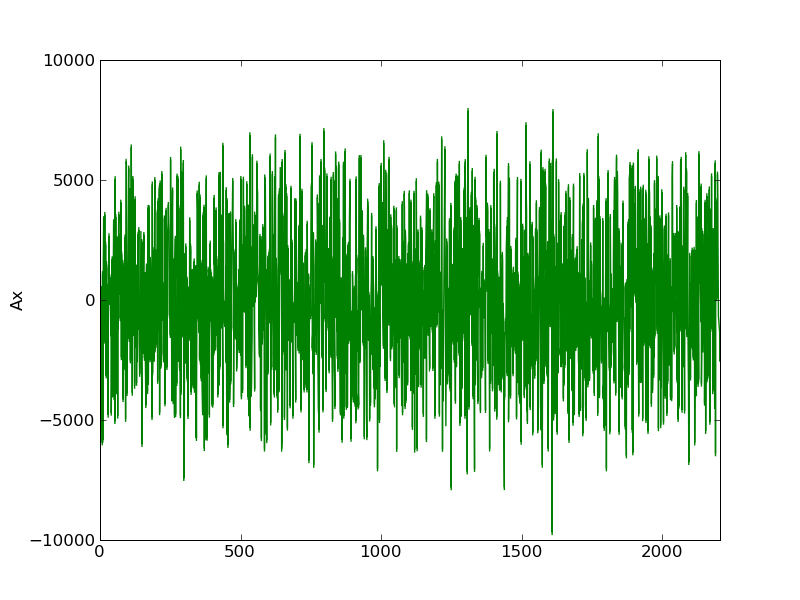
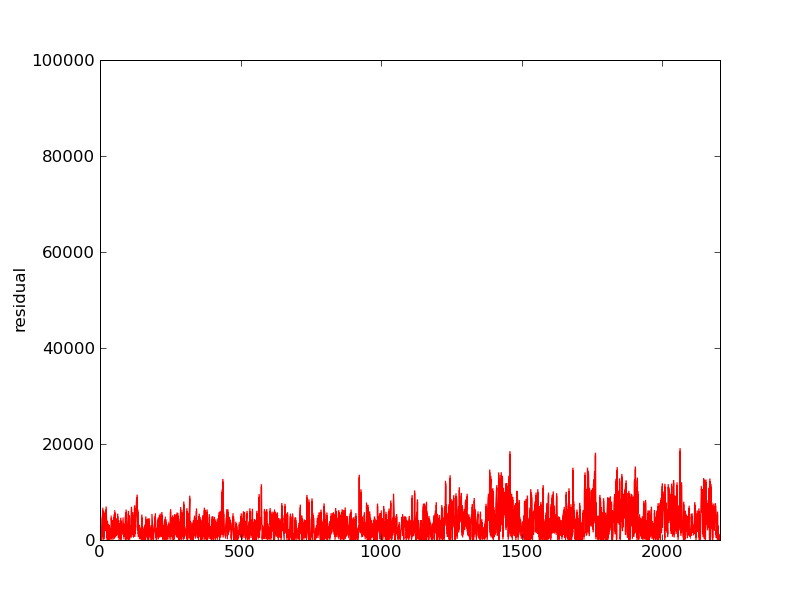
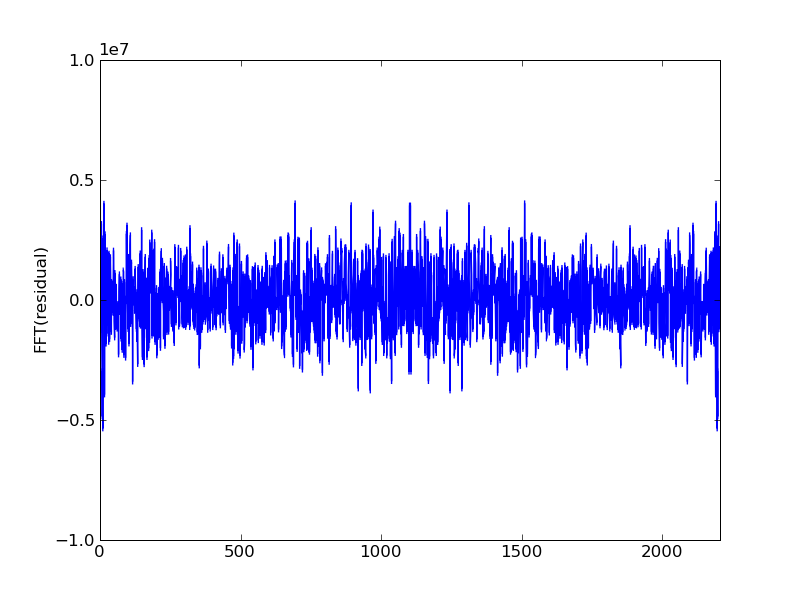
After one iteration the high notes become audible gauss_seidel_out000000.wav

And some structure is visible in the spectrum:

Second iteration: gauss_seidel_out000001.wav


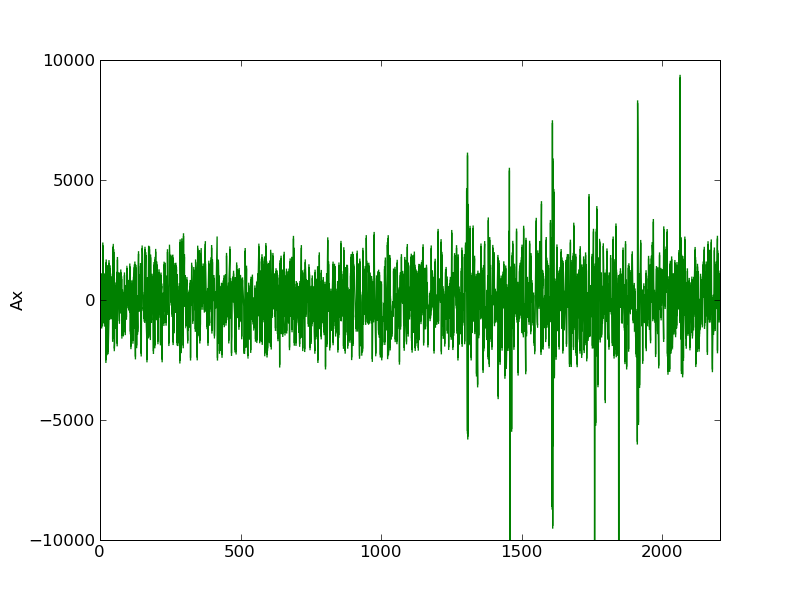
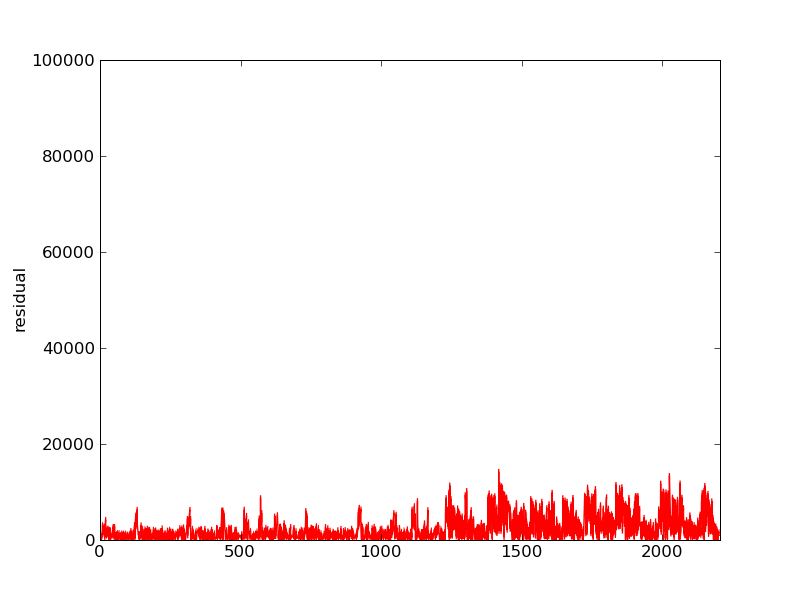
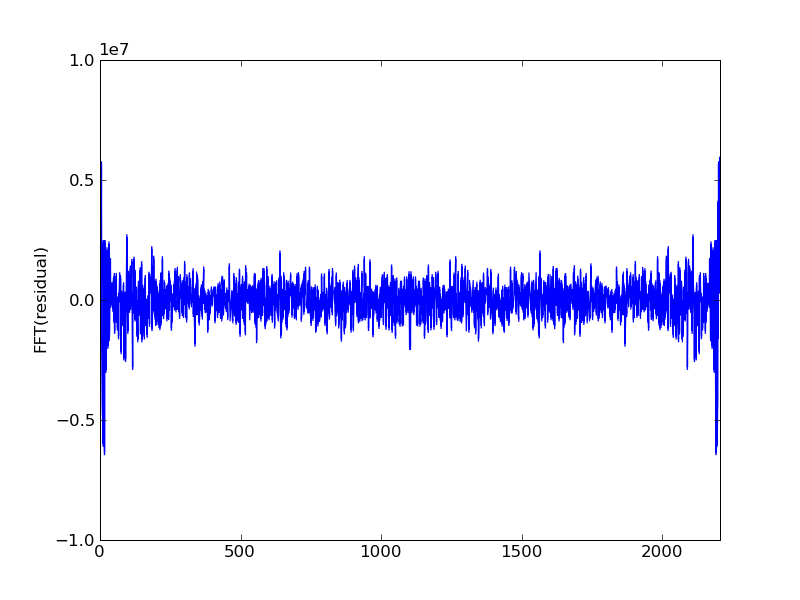
Third iteration: gauss_seidel_out000002.wav

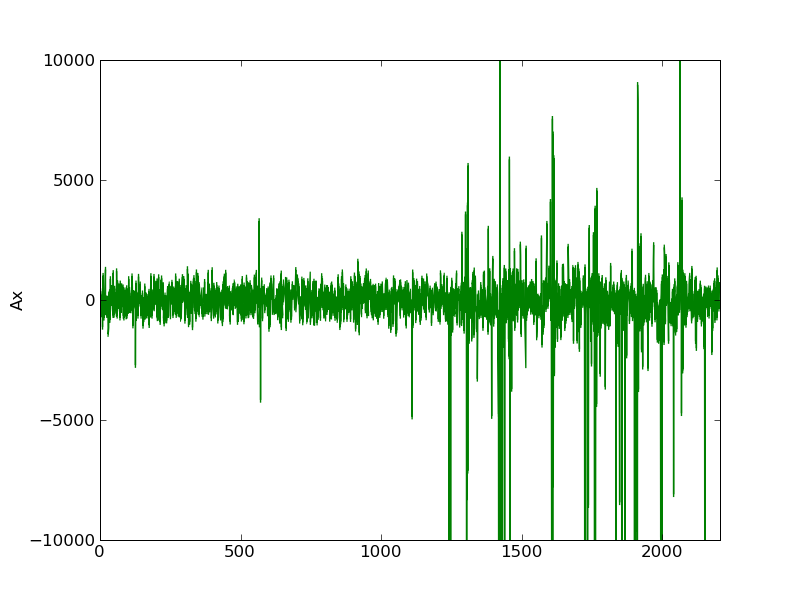
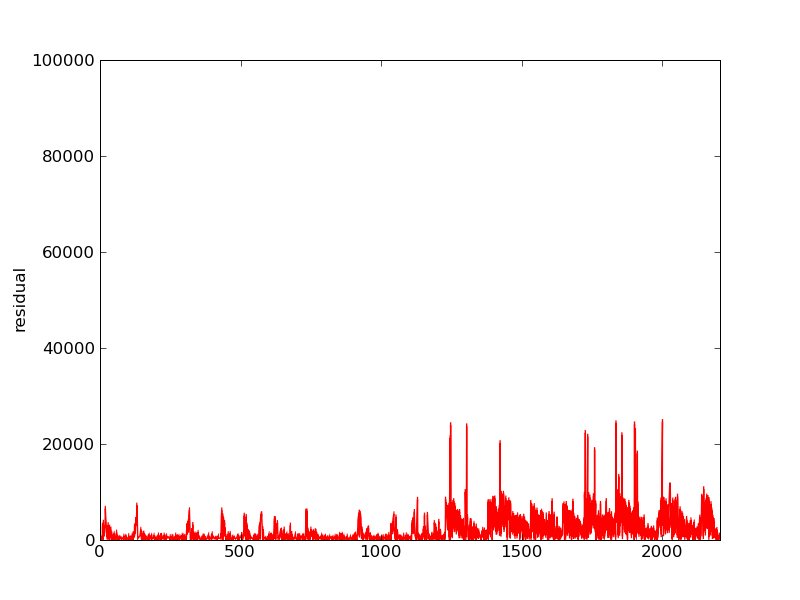
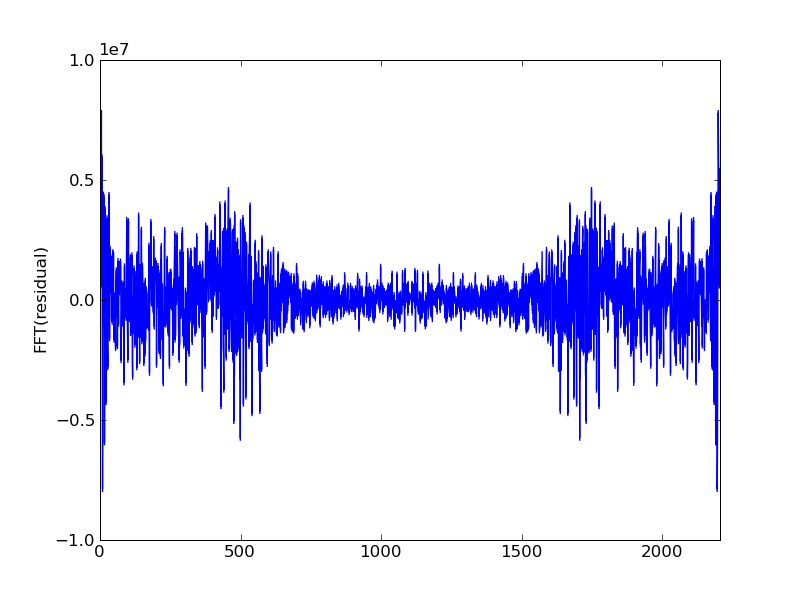
Fourth iteration: gauss_seidel_out000003.wav

This is all done in python. Loading .wav files into arrays is not too bad in scipy. A sparse matrix class is neccessary to avoid memory problems as a 12 second .wav file needs an array of size 12*44100. Here's the TridiagonalMatrix class I used: 

from numpy import *

#a tridiagonal matrix class
class TridiagonalMatrix:
    #initialize with 3 numpy arrays
    def __init__(self, upper_in, diag_in, lower_in):
        self.upper  = upper_in
        self.diag   = diag_in
        self.lower  = lower_in
        self.dim    = diag_in.shape[0]
    #matrix mulitplication
    def apply(self, v):
        out = ndarray(self.dim)
        try:
            out[0] = self.diag[0]*v[0] + self.upper[0]*v[1]
            out[self.dim-1] = self.lower[self.dim-2]*v[self.dim-2] + self.diag[self.dim-1]*v[self.dim-1]
            for i in range(1, self.dim-1):
                out[i] = self.lower[i-1]*v[i-1] + self.diag[i]*v[i] + self.upper[i]*v[i+1]
        except(IndexError):
            print "Wrong sizes"

        return out

    #solve Ax=b using gauss seidel
    #with initial guess x0
    def gauss_seidel(self, b, x0, tol):
        error = self.apply(x0) - b
        x = x0
        count=0
        while(linalg.norm(error) > tol):
            #update x in place
            x[0] = (b[0] - self.upper[0]*x[1])/self.diag[0]
            x[self.dim-1] = (b[self.dim-1] - self.lower[self.dim-2]*x[self.dim-2])/self.diag[self.dim-1]
            for i in range(1,self.dim-1):
                x[i] = (b[i] - self.lower[i-1]*x[i-1] - self.upper[i]*x[i+1])/self.diag[i]
            #update the error
            error = self.apply(x) - b

            count = count+1
            print count
        return x
And here's the code to handle reading/writing the .wav files and then using Gauss-Seidel to iteratively solve a linear system: 
from TridiagonalMatrix import *
from numpy import *
from scipy.io import wavfile
import scipy.fftpack
import pylab
import sys
import os

def musical_gauss_seidel(A, b, x0, tol):
"""
do the gauss seidel iteration
but output some sound every now and then..
A is some matrix that lets gauss seidel work
b is a vector that represents a .wav file of a pretty song
x0 is our initial guess for the gauss seidel method (probably random static)
we are going to output the .wav data corresponding to Ax
as Ax gets closer to b (ie the residual gets smaller)
we should hear the song emerge from the initial guess
"""
    #make noise of the initial approximation to b
    wavfile.write("gauss_seidel_out000000.wav", 44100, (A.apply(x0)).astype(int16))

    residual  = A.apply(x0) - b

    Ax = A.apply(x0)
    Ax = Ax.astype(int16)
    wavfile.write("initialAx.wav", 44100, Ax)

    x = x0
    count=0
    while(linalg.norm(residual) > tol):
        #update x in place
        x[0] = (b[0] - A.upper[0]*x[1])/A.diag[0]
        x[A.dim-1] = (b[A.dim-1] - A.lower[A.dim-2]*x[A.dim-2])/A.diag[A.dim-1]
        for i in range(1,A.dim-1):
            x[i] = (b[i] - A.lower[i-1]*x[i-1] - A.upper[i]*x[i+1])/A.diag[i]

        #this will approx b...
        Ax = A.apply(x)
        Ax = Ax.astype(int16)

        #update the reisdual, and get its fft for a nice photo
        residual = Ax - b

        #plot Ax (or something else, the fft of error should be cool...)
        #pylab.plot(Ax)
        pylab.plot(arange(len(Ax)), scipy.fftpack.fft(residual), label="FFT of Ax-b")

        pylab.savefig("AxFFT"+str(count).zfill(6)+".png")

        print "step: ", count, " residual norm: ", linalg.norm(residual)
        #slow convergence so dont write too much
        #if( count%50 == 0):
        wavfile.write("gauss_seidel_out"+ str(count).zfill(6)+".wav", 44100, Ax)

        count = count+1
    return x


def usage():
    print "Usage:  %s" % os.path.basename(sys.argv[0]) + " s x0.wav b.wav"
    print "Where s is the number of seconds to CG."
    print "and x0.wav is the first approximation to b"
    print "and b.wav is what we will converge to"
    return


def main():
"""
you need 3 arguments to main
the first is the number of seconds
the second is the intial guess x0
the 3rd is the song
"""
    args = sys.argv[1:]
    if "-h" in args or "--help" in args:
        usage()
        sys.exit(2)

    seconds = double(args[0])

    #read all the data from each wavfile
    #into a tuple
    #first argument is initial guess (probably random.wav)
    x0_name = args[1]
    x0_wav_data = wavfile.read(x0_name)

    #b is a pretty song that we will approximate
    b_name = args[2]
    b_wav_data = wavfile.read(b_name)

    #the first element in the tuple is the sample rate
    x0_sample_rate = x0_wav_data[0]
    b_sample_rate = b_wav_data[0]
    if x0_sample_rate != b_sample_rate:
        print "need both to have same sample rate"
        exit(2)
    sample_rate = b_sample_rate
    print sample_rate, "the sample rate of b"

    #b,x from Ax=b
    #forget about stereo sound for all this
    #choose the first column...
    #wont work for more than 2 channels
    print b_wav_data[1].shape, "shape of .wav read into b"
    print x0_wav_data[1].shape, "shape of .wav read into x0"
    if len(b_wav_data[1].shape) == 1:
        b = b_wav_data[1]
    elif len(b_wav_data[1].shape) == 2:
        b = b_wav_data[1][:,0]
    else:
        print "I don't know about 3 channels..."
        exit(2)

    #read in x0 as long as it has 2 or less channels..
    if len(x0_wav_data[1].shape) == 1:
        x0 = x0_wav_data[1]
    elif len(x0_wav_data[1].shape) == 2:
        x0 = x0_wav_data[1][:,0]
    else:
        print "I don't know about 3 channels..."
        exit(2)

    #how big the arrays are
    N = seconds*sample_rate
    N = int(N)

    b = b[0:N]
    x0 = x0[0:N]
    N = b.shape[0]#err
    print N, "the length of the arrays after some kinda subsampling"

    #make white noise as the initial guess.
    for i in range(len(x0)):
        x0[i] = random.randint(1,10768)

    #form a tridiagonal matrix
    #you get faster convergence for big diagonals
    A = TridiagonalMatrix(ones(N-1), zeros(N), ones(N-1))
    for i in range(N):
        A.diag[i] = -2.001

    print b.size, "b size"
    print x0.size, "x0 size"

    tol = 1000
    x = musical_gauss_seidel(A, b , x0, tol)

    return

if __name__== "__main__":
    main()